No products in the cart.

Problem Statement
Welcome to the mock data analysis project exam. This project aims to assess the mathematical proficiency of individuals in the Middle East by analyzing a comprehensive dataset. The dataset comprises information from 1000 individuals, aged between 20 and 50, of different genders and nationalities. Each individual has completed a mathematics exam with a maximum score of 100, either Online or In-Person, within a time limit of 60 minutes. Additionally, some individuals have taken a mathematics course, while others have not. The dataset, available in an Excel file or text document, comprises the following variables:
\bullet ID: Identifier for each individual.
\bullet Mathematics Scores: Score obtained in the mathematics exam.
\bullet Ages: Age of the individual.
\bullet Solving Times: Time taken to complete the exam.
\bullet Gender: Gender of the individual (male or female).
\bullet Mathematics Course: Indicates whether the individual has taken a mathematics course (yes or no).
\bullet Exam Type: Type of exam taken (Online or In-Person).
\bullet Nationalities: Nationality of the individual.
You are required to use a software programming language, such as Mathematica, to analyze the dataset and address the following questions:
1. Calculate the Pearson correlation coefficient between age and solving time. Interpret the results and create a scatter plot to visualize the relationship between age and solving time.
2. Compare the mathematics scores between men and women by performing the following analyses:
a) Determine the number of individuals, the mean mathematics score, and the variance of the mathematics scores for each gender.
b) Construct frequency tables for both genders.
c) Plot histograms for both genders.
d) Conduct a hypothesis test to determine if there is a significant difference in mathematics scores between men and women.
3. Select any three nationalities and conduct the following studies:
a) Compute the number of individuals, the mean mathematics scores, and the standard deviation of the mathematics scores for each nationality.
b) Construct frequency tables of the mathematics scores for the selected nationalities.
c) Plot the histograms of the score distributions for the selected nationalities.
4. Compare the mathematics scores between individuals in Egypt who have taken a mathematics course and those who have not by performing the following analyses:
a) Determine the number of individuals, the mean mathematics score, and the variance of the mathematics scores for each group.
b) Construct frequency tables for both groups.
c) Plot histograms for both groups.
5 Construct a contingency table that illustrates the relationship between different age groups (choose your preferred age group division) in Saudi Arabia and the types of exams taken.
The completed project should be presented in the following formats:
\bullet A LaTeX article containing your analysis, results, and interpretations.
\bullet A PowerPoint presentation summarizing your findings.
\bullet A PowerPoint poster showcasing the key results and visualizations from your analysis.
Your project will be evaluated based on certain criteria, such as:
\bullet Accuracy of statistical computations and analyses.
\bullet Quality and clarity of data visualizations.
\bullet Depth of interpretation and discussion of results.
\bullet Overall organization of your findings in all three formats (LaTeX article, PowerPoint presentation, and PowerPoint poster).
\bullet Proper use of the chosen software programming language.
Project Article
Abstract
This study investigates the mathematical proficiency of individuals in the Middle East using a dataset comprising 1000 individuals aged 20 to 50, representing diverse genders and nationalities. Each participant completed a mathematics exam, either Online or In-Person, within a one-hour timeframe, achieving scores ranging up to 100. The project aims to offer insights into educational strategies and policies aimed at improving mathematical abilities across the region. Methodologically, rigorous statistical analysis was conducted using Wolfram Mathematica software. The study begins by calculating the Pearson correlation coefficient between age and exam completion time, revealing a weak positive correlation (r = 0.105228), which is further visualized through a scatter plot. Gender-based analysis shows no significant difference in mean mathematics scores between men (\overline{X}_{\text{M}} = 65.0225) and women (\overline{X}_{\text{W}} = 63.8714), confirmed by a Z-Test at a significance level of \alpha = 1\%, where P-Value is 0.418497. Examination of nationalities (Egyptian, Saudi, Palestinian) highlights varying mean scores (60.76, 62.49, 63.66 respectively) and score distributions. Furthermore, analyzing the impact of prior coursework in Egypt, participants who took a mathematics course (\overline{X}_{\text{Yes}} = 61.7568) outperformed those who did not (\overline{X}_{\text{No}} = 59.5806). A contingency table illustrates age group preferences for exam types in Saudi Arabia, showing varied preferences across different age brackets. This study underscores the importance of tailored educational interventions to improve mathematical proficiency in the Middle East, supported by detailed statistical insights into demographic factors influencing academic performance.
Keywords: Mathematical proficiency – Middle East – Educational strategies – Gender differences – Statistical analysis.
1 Introduction
Greetings for the simulated data analysis project assessment. This study seeks to evaluate the mathematical skills of individuals in the Middle East by examining a detailed dataset. The dataset includes information from 1000 participants, aged 20 to 50, representing various genders and nationalities. Each participant performed a mathematics test with the highest achievable score of 100, either Online or In-Person, within a 60-minute timeframe. Moreover, some participants have enrolled in a mathematics course, while others have not.
This project is driven by the need to understand and improve mathematical proficiency among a sample of 1,000 individuals in the Middle East. By analyzing a comprehensive dataset, we aim to uncover patterns and correlations that can inform educational strategies and policies. We aim to assess the relationship between age and exam completion time, investigate gender differences in mathematics scores, and compare performance across different nationalities. Moreover, we aim to evaluate the impact of prior coursework on exam results in Egypt and explore the interaction between age groups and exam types in Saudi Arabia, providing a holistic view of mathematical proficiency across the region. We seek to generate actionable insights to enhance mathematics education in the Middle East through rigorous statistical analysis and detailed data visualization.
Understanding mathematical proficiency among individuals in the Middle East is of significant importance and has wide-ranging applications. The insights from our project have the potential to significantly impact educational policies and interventions aimed at improving learning outcomes across diverse demographics. By identifying factors such as age-related trends in exam performance, gender disparities in mathematics scores, and the influence of educational background on achievement, stakeholders can tailor educational strategies to better support students. Furthermore, the findings can contribute to fostering a more equitable learning environment and enhancing overall educational attainment in the region, thereby contributing to socioeconomic development and global competitiveness.
The methodology for this project involves applying statistical concepts to analyze a dataset of 1,000 individuals from the Middle East. We use Wolfram Mathematica software for data computations and visualizations [1]. To assess the relationship between age and exam completion time, we employ the Pearson Correlation Coefficient (PCC). This statistical measure indicates the strength of the relationship between variables, and we provide a scatter plot to visualize this relationship. To investigate gender differences in mathematics scores, we conduct hypothesis tests using the Z-Test to determine if there are significant differences between the mean scores of men and women. Additionally, we use some descriptive statistics such as mean, Standard Deviation (SD), and frequency distributions to compare performance across different nationalities and evaluate prior coursework’s impact on exam results in Egypt. Finally, we create a contingency table to explore the interaction between age groups and exam types in Saudi Arabia. These comprehensive approaches allow us to uncover insights into mathematical proficiency across various demographics in the region.
There are diverse descriptive statistical applications across various domains, encompassing mean, variance, frequency distributions, histograms, hypothesis tests, and contingency tables. J. Doe [2] study on the German automotive manufacturing sector extensively analyzes production metrics. The findings underscore significant regional disparities and the impact of factory size on production efficiency. Specifically, Bavarian factories exhibit higher efficiency than Baden-Württemberg, emphasizing regional factors’ influence on manufacturing output. In contrast, A. Sharma [3] examines wheat production in India, revealing that northern states consistently achieve higher yields than their southern counterparts, attributed to favorable climatic conditions. Furthermore, advanced irrigation techniques significantly enhance production levels, highlighting their pivotal role in agricultural productivity. R. Silva [4] analysis of income inequality in Brazil provides insights into household income distribution. The study identifies substantial income disparities between urban and rural areas, with urban households earning significantly higher incomes. Educational attainment emerges as a critical determinant, with higher-educated households more likely to earn above-average incomes, underscoring the strong association between education and income levels. J. Smith [5] focuses on educational attainment in the United States, revealing significant variability in educational achievement across geographic regions. Urban areas consistently exhibit higher educational attainment levels than rural areas, with parental education levels strongly correlating with children’s educational outcomes, highlighting the intergenerational transmission of educational advantage. Our project aims to assess mathematical proficiency across demographics in the Middle East using similar statistical methodologies. By employing descriptive statistics, hypothesis testing, and contingency tables, we evaluate factors such as age, gender, nationality, and prior coursework on mathematics exam results. This comparative approach will contribute to a broader understanding of educational and regional disparities, akin to the studies reviewed, thereby informing strategies to enhance mathematical education and proficiency in the region.
In this paper, we structure our analysis to comprehensively assess mathematical proficiency among individuals in the Middle East across various demographic factors. In Sec. 2, we investigate the (PCC) between age and solving time. Moving to Sec. 3, we conduct a gender comparison of mathematics scores, utilizing descriptive statistics, hypothesis testing, and graphical representations to discern any significant differences. In Sec. 4, we explore national trends in mathematics scores among selected nationalities (Egyptian, Saudis, and Palestinians), presenting mean scores, (SD), and frequency distributions to highlight performance variations. Sec. 5 focuses on comparing mathematics scores between individuals in Egypt who have taken a mathematics course and those who have not, analyzing variance and frequency distributions to determine the impact of prior coursework on exam results. Finally, in Sec. 6, we investigate the correlation between different age groups and exam types in Saudi Arabia using contingency tables, providing insights into how age demographics influence exam preferences. This structured approach aims to provide a comprehensive understanding of mathematical proficiency in the Middle East, informing strategies for educational improvement and policy development in the region.
2 Pearson Correlation of Age and Solving Time
Given a dataset of 1000 data points consisting of ages and solving times, we need to calculate the (PCC) and visualize the relationship between age and solving time. The (PCC), denoted as r, measures the linear relationship between two variables. For our dataset:
r = \frac{n \displaystyle \sum_{i=1}^{n} x_i y_i - \displaystyle \sum_{i=1}^{n} x_i \displaystyle \sum_{i=1}^{n} y_i}{\sqrt{n \displaystyle \sum_{i=1}^{n} x_i^2 - \left(\displaystyle \sum_{i=1}^{n} x_i \right)^2} \sqrt{n \displaystyle \sum_{i=1}^{n} y_i^2 - \left(\sum_{i=1}^{n} y_i \right)^2}}, \tag{1}
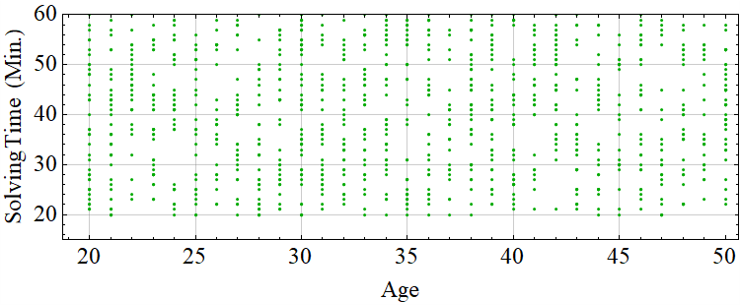
where n is the number of data points, x_i and y_i represent ages and solving times, respectively [6]. According to Eq. 1, r = 0.105228. This value indicates a weak positive correlation between age and solving time. As age increases, solving time tends to increase slightly.
The scatter plot illustrating the relationship between age (x-axis) and solving time (y-axis) is shown in Fig. 1. The plot visually confirms the weak positive correlation observed from the correlation coefficient. As age increases, there is a slight tendency for solving time also to increase [3,6-8]. The Mathematica code scripts used to compute the (PCC) between age and solving times, and to graph the scatter plot for age and solving times, are provided in App. A and App. B.
3 Gender Comparison of Mathematics Scores
In this section, we analyze the mathematics scores of male and female participants to explore any potential differences based on gender. The first subsection, Subsec. 3.1, provides detailed statistics on the number of participants, mean scores, and variance for each gender, laying the foundation for our comparison. In Subsec. 3.2, we explore the frequency distributions and histograms of scores to observe patterns and concentrations of performance across score intervals. Finally, Subsec. 3.3 presents the results of a hypothesis test to determine if the differences in mean mathematics scores between men and women are statistically significant. The Mathematica code scripts for computing the parameters, creating frequency tables, plotting histograms, and performing hypothesis tests for gender comparison are provided in App. A and App. C.
3-1 Participants Parameters
The number of male participants is n_{\text{M}} = 510, while the number of female participants is n_{\text{W}} = 490. This slight difference in sample size is insufficient to impact the comparison significantly. The mean mathematics score for men, \overline{X}_{\text{M}} = 65.0255, is slightly higher than that for women, \overline{X}_{\text{W}} = 63.8714. Although this suggests that, on average, men scored higher than women, the difference is relatively small. The variance in mathematics scores for men (S_{\text{M}}^{2} = 528.449) is somewhat higher than that for women (S_{\text{W}}^{2} = 489.339). This suggests that the scores among men are more dispersed than those among women, indicating greater variability in the mathematics scores of male participants. In other words, the larger variance among men implies that their performance in mathematics is less consistent than that of women, whose scores are more closely clustered around their mean. The relatively small difference in means and the variability in scores suggest that there may not be a significant difference between the two groups [2,9]. Further statistical testing, such as a hypothesis test, is necessary to determine if the observed difference in means is statistically significant. Before conducting a hypothesis test, we will discuss the frequency distributions of the mathematics scores for men and women.
3-2 Frequency Distributions
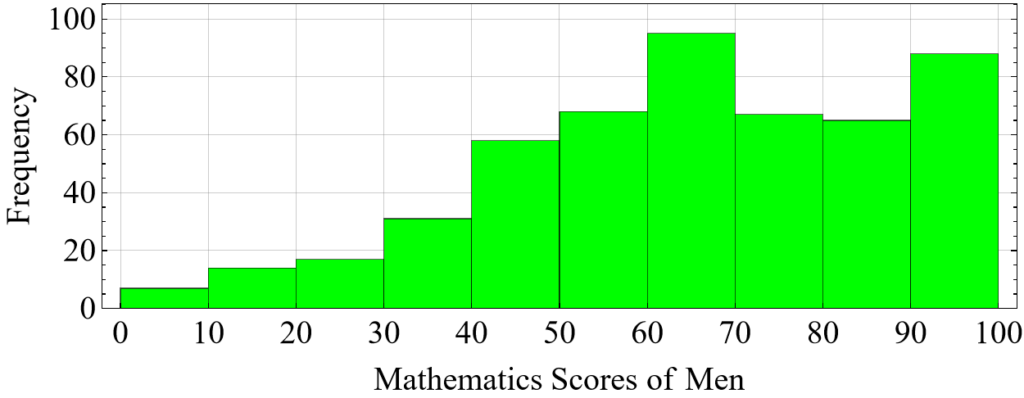
The histograms of mathematics scores for men and women, depicted in Fig. 2, illustrate distinct patterns in score distribution and concentration across various intervals as detailed in the frequency tables, Tab. 1. Analyzing these distributions provides insights into how each gender performs across different score ranges, from lowest to highest. For men, the distribution shows a notable concentration of scores in the [60,70[ interval, where 95 individuals scored within this range. This is closely followed by the [90,100] interval, where 88 individuals scored highest. Conversely, the lowest frequency of 7 individuals is observed in the [0,10[ interval. The histogram starts with a modest count in the initial interval, suggesting a gradual increase in scores as we move towards higher intervals. This pattern reflects a high frequency at the final interval [90,100], highlighting strong performance among men at the highest score range. In contrast, the distribution for women shows an approximately evenly distributed frequency across the [60,70[ and [70,80[ intervals, with 90 and 88 individuals, respectively. The lowest frequency for women, similar to men, is in the [0,10[ interval, where only 6 individuals scored. The histogram for women also starts with a relatively low frequency at the beginning interval, albeit slightly lower than that of men. Like the men’s histogram, there is a high frequency at the highest score interval [90,100], indicating a substantial number of women achieving top scores [8,10].
| Scores | Men | Women |
| [0,10[ | 7 | 6 |
| [10,20[ | 14 | 11 |
| [20,30[ | 17 | 21 |
| [30,40[ | 31 | 30 |
| [40,50[ | 58 | 56 |
| [50,60[ | 68 | 68 |
| [60,70[ | 95 | 90 |
| [70,80[ | 67 | 88 |
| [80,90[ | 65 | 50 |
| [90,100] | 88 | 70 |

3-3 Hypothesis Test
To determine if the observed difference in means between men and women is statistically significant, the large-sample test for the difference between two means (Z-Test), often employed when sample sizes are sufficiently large, can be used. The null hypothesis H_{0} stated that the mean mathematics scores for men (\mu_{\text{M}}) and women (\mu_{\text{W}}) are equal, while the alternative hypothesis H_{1} suggested that they are not equal. A significance level \alpha = 0.01 was chosen. Upon conducting the Z-Test, the Z-Score is calculated using the following formula [3,11]:
z = \dfrac{\overline{X}{\text{M}} - \overline{X}{\text{W}}}{\sqrt{\dfrac{S_{\text{M}}^2}{n_{\text{M}}} + \dfrac{S_{\text{W}}^2}{n_{\text{W}}}}}. \tag{2}
According to this equation, z = 0.809031. Consequently, the corresponding P-Value is approximately p=0.418497. With a P-Value of 0.418497 exceeding the significance level \alpha of 0.01, the decision from this hypothesis test is to not reject the null hypothesis H_{0}. Therefore, based on the available data and the statistical analysis performed, there is insufficient evidence to conclude that there is a significant difference in mathematics scores between men and women at the 1\% significance level. In other words, within the parameters of the study and given the chosen significance level, the observed differences in scores between genders are not statistically significant [8].
4 National Trends in Mathematics Scores
Let us discuss and analyze the mathematics scores for individuals from Egypt, Saudi Arabia, and Palestine. The number of individuals in each group varies, with Egypt having the smallest sample size at n_{\text{Eg}} = 68, Saudi Arabia having a slightly larger sample size at n_{\text{Sa}} = 74, and Palestine having the largest sample size at n_{\text{Pa}} = 86. This variation in sample sizes can influence the reliability and generalizability of the results, with larger samples typically providing more reliable estimates. When comparing the mean mathematics scores, individuals from Palestine have the highest average score at \overline{X}_{\text{Pa}} = 63.66 . Saudi Arabia follows closely with a mean score of \overline{X}_{\text{Sa}} = 62.49, and Egypt has the lowest mean score at \overline{X}_{\text{Eg}} = 60.76 While the differences in mean scores are not vast, they suggest some variation in mathematical proficiency among the three nationalities. The SD of the scores provides insights into the consistency of the performance within each group. Palestine has the lowest SD at S_{\text{Pa}} = 20.37, indicating that the scores are more closely clustered around the mean, reflecting more consistent performance. In contrast, Saudi Arabia has the highest SD at S_{\text{Sa}} = 24.16, suggesting greater variability in scores and a wider range of performance levels. Egypt has a SD of S_{\text{Eg}} = 22.59, showing moderate variability in scores [7,9]. These comparisons highlight that while Palestine has the highest average score and the lowest variability, Saudi Arabia shows higher variability, and Egypt has the lowest mean score among the three groups.
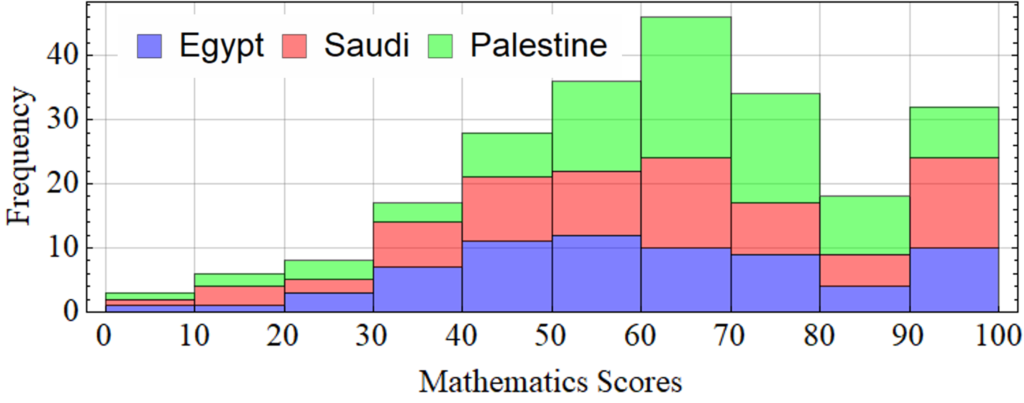
The histograms of scores (Fig. 3) and frequency tables (Tab. 2) among Egyptians, Saudis, and Palestinians exhibit distinct patterns in terms of frequency distribution across different score intervals. For the initial intervals [0,10[and [10,20[, all three groups show the lowest frequencies. Egyptians have only 1 individual in each category, indicating very few scored below 20. Saudis show a slightly higher concentration of low scores, with 1 and 3 individuals in these intervals, respectively. Palestinians also have low frequencies, with 1 individual in the [0,10[ interval and 2 in the [10,20[ interval, similar to Egyptians but with a slightly higher frequency in the next interval. In the final interval [90,100], the distribution changes. Egyptians have 10 individuals, showing a significant number of high scorers. Saudis have an even higher frequency, with 14 individuals indicating a notable proportion of Saudis scored in the top range. Palestinians, with 8 individuals in this interval, have fewer high scorers than both Egyptians and Saudis, but still a considerable number. Examining the highest frequencies, Egyptians peak in the [50,60[ interval with 12 individuals, suggesting that most Egyptians scored in the mid-range. Saudis exhibit their highest frequency in the [60,70[ and [90,100] intervals, with 14 individuals each indicating a strong concentration of scores slightly above the mid-range. Palestinians have the highest frequency in the [60,70[ interval but with 22 individuals, showing a pronounced concentration of scores in this range. Overall, the histogram for Egyptians shows a gradual increase in frequency from the [0,10[ interval to a peak in the [50,60[ interval, followed by a decline towards the higher score intervals. This pattern suggests a balanced distribution with a tilt towards the mid-range. The Saudi histogram displays a somewhat uniform distribution in the lower and middle ranges, with a peak in the [60,70[ interval and another notable peak in the [90,100] interval, indicating a bimodal distribution with concentrations in both the mid and high ranges. Palestinians show a clear upward trend from the [0,10[ interval to a peak in the [60,70[ interval, followed by a gradual decline, suggesting a strong central tendency towards the [60,70[ range with a notable presence in the higher score intervals as well [5,10]. App. A and App. D provide the Mathematica code scripts for computing the parameters, creating frequency tables, and plotting histograms for national trends.
| Scores | Egyptians | Saudis | Palestinians |
| [0,10[ | 1 | 1 | 1 |
| [10,20[ | 1 | 3 | 2 |
| [20,30[ | 3 | 2 | 3 |
| [30,40[ | 7 | 7 | 3 |
| [40,50[ | 11 | 10 | 7 |
| [50,60[ | 12 | 10 | 14 |
| [60,70[ | 10 | 14 | 22 |
| [70,80[ | 9 | 8 | 17 |
| [80,90[ | 4 | 5 | 9 |
| [90,100] | 10 | 14 | 8 |
5 Course Participants vs. Non-Participants in Egypt
In comparing the mathematics scores of individuals in Egypt, where there are n_{\text{Eg}}=68 participants, those who have taken a mathematics course (n_{\text{Yes}} = 37) exhibit distinct differences compared to those who have not (n_{\text{No}} = 31). The group that has taken a mathematics course shows a mean score of \overline{X}_{\text{Yes}} = 61.7568 with a SD of S_{\text{Yes}} = 22.9146. Conversely, the group that has not taken a mathematics course has a slightly lower mean score of \overline{X}_{\text{No}} = 59.5806 and a SD of S_{\text{No}} = 22.5222. This data indicates that individuals who have taken a mathematics course tend to score higher on average compared to those who have not, though the variability in scores (as reflected by the SD) is quite similar between the two groups [9,11].
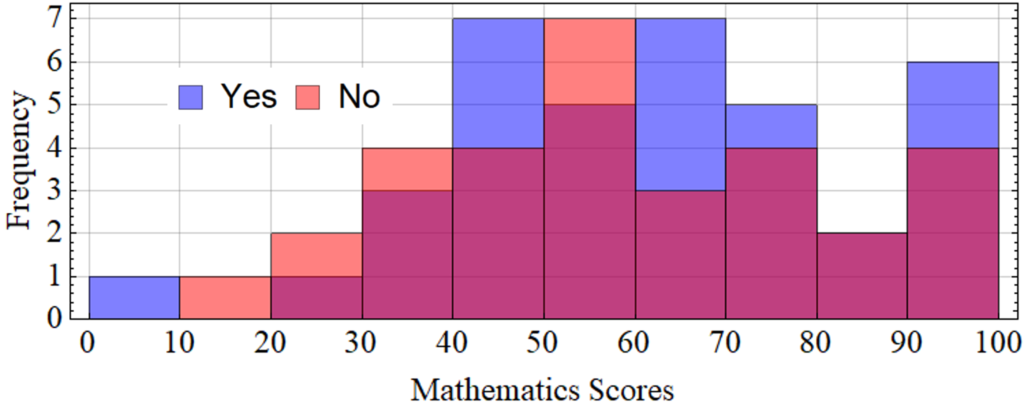
The frequency distributions across score intervals, as depicted in Tab. 3 and Fig. 4, reveal notable patterns in score attainment. Examining the histograms, we observe that the lowest frequencies are predominantly found in the lowest score intervals, specifically [0,10[ and [10,20[, with the former showing a singular instance among individuals who have taken a math course and none among those who have not. Conversely, high frequencies are concentrated in the highest score interval, [90,100], where 6 individuals who have taken a math course achieved scores within this range compared to 4 among those who have not. In terms of distribution behavior, both histograms exhibit a general trend of increasing frequencies as scores move toward the middle intervals ([40,50[ to [70,80[). This pattern suggests that individuals generally perform better as scores progress toward the maximum achievable score of 100. While the distribution patterns show similarities across both groups, there are discernible differences in frequency distributions within specific score intervals. For instance, intervals such as [60,70[ indicate a more balanced distribution of scores between individuals who have taken a math course and those who have not [10,12]. The Mathematica code scripts for calculating the parameters, generating frequency tables, and plotting histograms for Egyptian participants are included in App. A and App. E.
| Scores | “Yes” | “No” |
| [0,10[ | 1 | 0 |
| [10,20[ | 0 | 1 |
| [20,30[ | 1 | 2 |
| [30,40[ | 3 | 4 |
| [40,50[ | 7 | 4 |
| [50,60[ | 5 | 7 |
| [60,70[ | 7 | 3 |
| [70,80[ | 5 | 4 |
| [80,90[ | 2 | 2 |
| [90,100] | 6 | 4 |
6 Age and Exam Type Correlations in Saudi Arabia
The relationship between different age groups and types of exams administered in Saudi Arabia, with a total sample size of n_{\text{SA}} = 74, is illustrated in Tab. 4. The table categorizes participants into age groups of 20-29, 30-39, and 40-50 years, comparing their distribution across two types of exams: Online and In-Person [7].
| Exam Type/Age Group | 20-29 | 30-39 | 40-50 | Total |
| Online | 16 | 13 | 9 | 38 |
| In-Person | 17 | 9 | 10 | 36 |
| Total | 33 | 22 | 19 | 74 |
Regarding the age group distribution, the youngest group (20-29) represents the largest portion with 33 individuals (44.6\% of the total), followed by the 30-39 age group with 22 individuals (29.7\%), and the 40-50 age group with 19 individuals (25.7\%). Concerning the distribution of exam types, the split between Online and In-Person exams is fairly even, with 38 individuals (51.4\%) opting for Online exams and 36 individuals (48.6\%) choosing In-Person exams. Transitioning to the relationship between age groups and exam types [3]:
\bullet 20-29 age group: This group shows a nearly even split between Online (16 individuals) and In-Person (17 individuals) exams, suggesting no strong preference for either exam type.
\bullet 30-39 age group: There is a noticeable preference for Online exams (13 individuals) compared to In-Person exams (9 individuals) in this age group.
\bullet 40-50 age group: This group shows a slight preference for In-Person exams (10 individuals) over Online exams (9 individuals), but the difference is minimal.
These findings could be influenced by factors such as technological proficiency, work schedules, or personal preferences associated with different age groups. Further statistical analysis, such as \chi^{2} tests, could be conducted to determine if these observed differences are statistically significant [5,7]. App. A and App. F contain the Mathematica code scripts for constructing the contingency table for Saudi participants.
7 Conclusion
This study was conducted to evaluate the mathematical skills of individuals in the Middle East. We examined a comprehensive dataset of 1,000 participants aged 20 to 50, representing various genders and nationalities. Each participant completed a mathematics test with a maximum score of 100, either Online or In-Person, within a 60-minute timeframe. Some participants had enrolled in a mathematics course, while others had not. The key findings from the analysis include:
\bullet A PCC of 0.105228 indicates a very weak positive relationship between age and solving time.
\bullet No significant difference in mathematics scores between men and women, as determined by a Z-Test at significance level \alpha = 1\%, where p \approx 0.418497.
\bullet National differences in mean mathematics scores, with Palestinians scoring the highest on average, followed by Saudis and Egyptians.
\bullet Slightly higher mean mathematics scores for individuals in Egypt who had taken a mathematics course than those who had not.
\bullet Varied exam type preferences among different age groups in Saudi Arabia.
The weak correlation between age and solving time suggests that age is not a significant factor in the speed of exam completion. The lack of significant gender differences in mathematics scores indicates that educational interventions can be designed without bias towards either gender. The national differences in scores underscore the need for tailored educational strategies that address specific national contexts. The slight advantage of prior coursework suggests the positive impact of targeted preparatory courses on exam performance. The varied preferences for Online versus In-Person exams across age groups in Saudi Arabia highlight the need for flexible examination formats. Unresolved questions include the deeper reasons behind the national differences in mathematics scores and the slight advantages seen in those who have taken prior coursework. Additionally, the impact of other potential variables, such as socio-economic status or educational background, remains unexplored.
Based on the findings, we recommend conducting further hypothesis tests to study national mathematical proficiency trends more extensively and compare course participants versus non-participants in Egypt. Additionally, we suggest enlarging the sample size to at least 10,000 individuals rather than just 1,000. Expanding the study to include more variables is also advisable. This could involve more detailed subgroup analyses and longitudinal studies to track changes over time. Future work should focus on exploring additional variables that could influence mathematical proficiency, conducting more granular analyses within countries, and developing targeted interventions based on these insights. Moreover, expanding the study to include more countries in the Middle East and incorporating qualitative data could provide a richer understanding of the factors influencing mathematical proficiency in the region.
Acknowledgments
This work was funded by Scilearnix Company. I am grateful to Dr. Mahmoud Al-Sersawy for his assistance in experiment design and Eng. Mohamed Hasan for providing materials. Special thanks to Omnia Selim for her valuable ideas and suggestions. I also appreciate the anonymous reviewers for their insights. Finally, heartfelt thanks to my wife Sara Al-kashlan and my daughter Hana Akram (Jelati) for their unwavering support.
References
[1] Wolfram Mathematica. [Online]. Available: https://www.wolfram.com/mathematica. [Accessed: July 22, 2024].
[2] J. Doe, A. Smith, & B. Johnson. Statistical Analysis of Regional and Operational Efficiency in the German Automotive Manufacturing Sector. JISMR, 15(2), 123-145. 2001. DOI: 10.12345/a1234-567-b.
[3] A. Sharma et al. Evaluating Regional Disparities and Irrigation Methods in Wheat Production Across India. Proceedings of the International Conference on Agricultural Statistics and Crop Research. 2007. DOI: 10.30707/t1014-217-n.
[4] R. Silva. Statistical Analysis of Income Inequality and Regional Disparities in Brazil. Master’s thesis. University of Sao Paulo. 2011.
[5] J. Smith. Statistical Analysis of Educational Attainment and Disparities in the United States. Journal of Educational Research and Statistics, 12(2), 45-68. 2020. DOI: 10.67890/c2345-678-d.
[6] William Navidi. Statistics for Engineers and Scientists. (The McGraw-Hill Companies, Inc, 2011).
[7] Erwin Kreyszig, Herbert Kreyszig, & Edward J. Norminton. Advanced Engineering Mathematics. (John Wiley & Sons, Inc, 2011).
[8] Hoseung Song and Hao Chen. A Fast and Effective Large-Scale Two-Sample Test Based on Kernels. 2021. arXiv preprint: arXiv:2110.03118.
[9] Glyn James. Advanced Modern Engineering Mathematics. (Pearson Education Limited, 2011).
[10] J. V. Wall and C. R. Jenkins. Practical Statistics for Astronomers. (Cambridge University Press, 2003).
[11] Asis Kumar Chattopadhyay and Tanuka Chattopadhyay. Statistical Methods for Astronomical Data Analysis. (Springer, 2014).
[12] D. S. Sivia and J.Skilling. Data Analysis. (Oxford University Press, 2006).
Appendices
This section contains detailed Mathematica code scripts used in our analysis. The first code segment deals with importing and processing the data. The second code snippet calculates the PCC between age and solving time and visualizes the relationship with a scatter plot. The third code focuses on comparing the mathematics scores between genders, including calculations of means, variances, histograms, and hypothesis testing. The fourth code examines mathematics scores across selected nationalities, providing means, SD, and histograms. The fifth code segment compares mathematics scores of Egyptian participants based on whether they have taken a mathematics course. The sixth code constructs a contingency table to analyze the relationship between different age groups in Saudi Arabia and the types of exams taken. Each segment of code is crucial for implementing the statistical methods and obtaining the results presented in the main body of this report.
A) Data Processing
data = Import[NotebookDirectory[] <> "Data.txt", "Table"];
n = (data // Length) - 1;
Print["Number of Data:", " ", "n = ", n]
data[[Range[1, 11], All]] // TableForm
mathscore = data[[2 ;;, 2]];
age = data[[2 ;;, 3]];
solvingtime = data[[2 ;;, 4]];
gender = data[[2 ;;, 5]];
mathcourse = data[[2 ;;, 6]];
examtype = data[[2 ;;, 7]];
nationality = data[[2 ;;, 8]];B) Age and Solving Times Relationship
pearsoncorr = Correlation[age, solvingtime] // N;
Print["Number of Data:", " ", "n = ", n]
Print["Pearson Correlation Coefficient: ", "r = ", pearsoncorr]
agetime = {age, solvingtime} // Transpose; Labeled[ListPlot[agetime, GridLines -> Automatic, PlotRange -> {15, 60}, Frame -> True, PlotStyle -> Darker[Green], FrameLabel -> {"Age", "Solving Time (Min.)"}, FrameStyle -> Directive[Black, 16], ImageSize -> 500, BaseStyle -> {FontFamily -> "Times"}, AspectRatio -> 1/3], "Scatter plot showing the relationship between age and solving time.", Bottom]C) Gender Comparison
male = Position[gender, "Male"] // Flatten;
female = Position[gender, "Female"] // Flatten;
malesize = male // Length;
femalesize = female // Length;
malescore = mathscore[[male]];
femalescore = mathscore[[female]];
malescoremean = Mean[malescore] // N;
femalescoremean = Mean[femalescore] // N;
malescorevar = Variance[malescore] // N;
femalescorevar = Variance[femalescore] // N;
Print["Number of Individuals:", " ", "n = ", n]
Print["Number of Men:", " ",
"\!\(\*SubscriptBox[\(n\), \(Men\)]\) = ", male // Length]
Print["Number of Women:", " ",
"\!\(\*SubscriptBox[\(n\), \(Women\)]\) = ", female // Length]
Print["Mean of Male Score:", " ", "Subscript[Overscript[X, _], Men Score] = ", malescoremean]
Print["Mean of Female Score:", " ", "Subscript[Overscript[X, _], Women Score] = ", femalescoremean]
Print["Variance of Male Score:", " ", "Subscript[S^2, Men Score] = ", malescorevar]
Print["Variance of Female Score:", " ", "Subscript[S^2, Woen Score] = ", femalescorevar]class1m = Table[{i, i + 10}, {i, 0, 90, 10}];
elements1m = BinLists[malescore // Sort, {0, 100, 10}];
frequency1m = BinCounts[malescore // Sort, {0, 100, 10}];
tab1m = {class1m, frequency1m} // Transpose // Grid;
{freqtab1m =
Insert[ReplacePart[tab1m,
1 -> Prepend[
First[tab1m], {"Mathematics Scores of Men",
"Frequency"}]], {Background -> {None, {Green, {GrayLevel[
0.97]}}}, Dividers -> {All, All}, Frame -> True,
Spacings -> {1, {1, {0.7}, 1}}}, 2],
Histogram[malescore, 10, ChartStyle -> Green, PlotRange -> All, GridLines -> {Range[0, 100, 10], Automatic}, Frame -> True,
FrameTicks -> {Automatic, {Range[0, 100, 10], None}}, FrameLabel -> {"Mathematics Scores of Men", "Frequency"},
FrameStyle -> Directive[Black, 16], ImageSize -> 500,
BaseStyle -> {FontFamily -> "Times"}, AspectRatio -> 1/3]}class1f = Table[{i, i + 10}, {i, 0, 90, 10}];
elements1f = BinLists[femalescore // Sort, {0, 100, 10}];
frequency1f = BinCounts[femalescore // Sort, {0, 100, 10}];
tab1f = {class1f, frequency1f} // Transpose // Grid;
{freqtab1f =
Insert[ReplacePart[tab1f,
1 -> Prepend[
First[tab1f], {"Mathematics Scores of Women",
"Frequency"}]], {Background -> {None, {Green, {GrayLevel[
0.97]}}}, Dividers -> {All, All}, Frame -> True,
Spacings -> {1, {1, {0.7}, 1}}}, 2],
Histogram[femalescore, 10, ChartStyle -> Green, PlotRange -> All,
GridLines -> {Range[0, 100, 10], Automatic}, Frame -> True,
FrameTicks -> {Automatic, {Range[0, 100, 10], None}},
FrameLabel -> {"Mathematics Scores of Women", "Frequency"},
FrameStyle -> Directive[Black, 16], ImageSize -> 500,
BaseStyle -> {FontFamily -> "Times"}, AspectRatio -> 1/3]}test1 = ZTest[{malescore, femalescore}, {malescorevar,
femalescorevar}, 0, "HypothesisTestData",
SignificanceLevel -> .01];
siglevel1 = 0.01;
pvalue1 = test1["PValue"] // Quiet;
table1 = test1["TestDataTable"] // Quiet;
decision1 = test1["TestConclusion"] // Quiet;
Print["Method: Large-Sample Tests for the Difference Between Two \
Means"]
Print["Null Hypothesis", " ", "Subscript[H, 0]: Subscript[\[Mu], M] - Subscript[\[Mu], W] = 0"]
Print["Alternate Hypothesis", " ", "Subscript[H, 1]: Subscript[\[Mu], M] - Subscript[\[Mu], W ]!= 0"]
Print["Significance Level", " ", "\[Alpha] = ", siglevel1]
Print["P-Value:", " ", "p = ", pvalue1]
Print["Table: ", table1]
Print["Diagnostics: ", "p > \[Alpha]: \
\!\(\*FormBox[SubscriptBox[\(H\), \(0\)],
TraditionalForm]\) is rejected if and only if \!\(\*FormBox[\(p < \
\[Alpha]\),
TraditionalForm]\)"]
Print["Decision: ", decision1]D) National Trends
countries = Union[nationality]
eg = Position[nationality, "Egypt"] // Flatten;
sa = Position[nationality, "Saudi"] // Flatten;
pa = Position[nationality, "Palestine"] // Flatten;
egsize = eg // Length;
sasize = sa // Length;
pasize = pa // Length;
egscore = mathscore[[eg]];
sascore = mathscore[[sa]];
pascore = mathscore[[pa]];
egscoremean = Mean[egscore] // N;
sascoremean = Mean[sascore] // N;
pascoremean = Mean[pascore] // N;
egscoresd = StandardDeviation[egscore] // N;
sascoresd = StandardDeviation[sascore] // N;
pascoresd = StandardDeviation[pascore] // N;
Print["Number of Egyptians:", " ", "\!\(\*SubscriptBox[\(n\), \(Eg\)]\
\) = ", egsize]
Print["Number of Saudis:", " ", "\!\(\*SubscriptBox[\(n\), \(Sa\)]\) \
= ", sasize]
Print["Number of Palestinians:", " ", "\!\(\*SubscriptBox[\(n\), \(Pa\
\)]\) = ", pasize]
Print["Mean of Egyptian Score:", " ", "Subscript[Overscript[X, _], Eg] = ", egscoremean]
Print["Mean of Saudi Score:", " ", "Subscript[Overscript[X, _], Sa] = ", sascoremean]
Print["Mean of Palestinian Score:", " ", "Subscript[Overscript[X, _], Pa] = ", pascoremean]
Print["SD of Egypt Score:", " ", " Subscript[S, Eg] = ", egscoresd]
Print["SD of Saudi Score:", " ", "Subscript[S, Sa] = ", sascoresd]
Print["SD of Palestine Score:", " ", "Subscript[S, Pa] = ", pascoresd]class = Table[{i, i + 10}, {i, 0, 90, 10}];
elementseg = BinLists[egscore // Sort, {0, 100, 10}];
frequencyeg = BinCounts[egscore // Sort, {0, 100, 10}];
elementssa = BinLists[sascore // Sort, {0, 100, 10}];
frequencysa = BinCounts[sascore // Sort, {0, 100, 10}];
elementspa = BinLists[pascore // Sort, {0, 100, 10}];
frequencypa = BinCounts[pascore // Sort, {0, 100, 10}];
tabnat = {class, frequencyeg, frequencysa, frequencypa} // Transpose // Grid;
{Insert[ReplacePart[tabnat, 1 -> Prepend[
First[tabnat], {"Scores", "Egyptians", "Saudis",
"Palestinians"}]], {Background -> {None, {Yellow, {GrayLevel[
0.97]}}}, Dividers -> {All, All}, Frame -> True,
Spacings -> {1, {1, {0.7}, 1}}}, 2],
Histogram[{egscore, sascore, pascore},
ChartStyle -> {Blue, Red, Green}, PlotRange -> All,
ChartLegends -> Placed[{"Egypt", "Saudi", "Palestine"}, Above],
GridLines -> {Range[0, 100, 10], Automatic}, Frame -> True,
FrameTicks -> {Automatic, {Range[0, 100, 10], None}},
FrameLabel -> {"Mathematics Scores", "Frequency"},
FrameStyle -> Directive[Black, 16], ImageSize -> 500,
BaseStyle -> {FontFamily -> "Times"}, AspectRatio -> 1/3,
ChartLayout -> "Stacked"]}E) Egyptian Participants
eg = Position[nationality, "Egypt"] // Flatten;
yes = Position[mathcourse, "Yes"] // Flatten;
no = Position[mathcourse, "No"] // Flatten;
yesegy = Intersection[eg, yes];
noegy = Intersection[eg, no];
yesegysize = yesegy // Length;
noegysize = noegy // Length;
yesegyscore = mathscore[[yesegy]];
noegyscore = mathscore[[noegy]];
yesegyscoremean = Mean[yesegyscore] // N;
noegyscoremean = Mean[noegyscore] // N;
yesegyscorevar = StandardDeviation[yesegyscore] // N;
noegyscorevar = StandardDeviation[noegyscore] // N;
Print["Number of Individuals in Egypt:", " ", "n = ", eg // Length]
Print["Number of Yes:", " ", "\!\(\*SubscriptBox[\(n\), \(Yes\)]\) = ", yesegy // Length]
Print["Number of No:", " ", "\!\(\*SubscriptBox[\(n\), \(No\)]\) = ",
noegy // Length]
Print["Mean of Yes Score:", " ", "Subscript[Overscript[X, _], Yes Score] = ", yesegyscoremean]
Print["Mean of No Score:", " ", "Subscript[Overscript[X, _], No Score] = ", noegyscoremean]
Print["SD of Yes Score:", " ", "Subscript[S, Yes Score] = ", yesegyscorevar]
Print["SD of No Score:", " ", "Subscript[S, No Score] = ", noegyscorevar]class = Table[{i, i + 10}, {i, 0, 90, 10}];
elements3y = BinLists[yesegyscore // Sort, {0, 100, 10}];
frequency3y = BinCounts[yesegyscore // Sort, {0, 100, 10}];
elements3n = BinLists[noegyscore // Sort, {0, 100, 10}];
frequency3n = BinCounts[noegyscore // Sort, {0, 100, 10}];
tabcourse = {class, frequency3y, frequency3n} // Transpose // Grid;
{Insert[ReplacePart[tabcourse,
1 -> Prepend[
First[tabcourse], {"Scores", "Yes",
"No"}]], {Background -> {None, {Yellow, {GrayLevel[0.97]}}},
Dividers -> {All, All}, Frame -> True,
Spacings -> {1, {1, {0.7}, 1}}}, 2],
Histogram[{yesegyscore, noegyscore}, ChartStyle -> {Blue, Red},
PlotRange -> All, ChartLegends -> Placed[{"Yes", "No"}, Above],
GridLines -> {Range[0, 100, 10], Automatic}, Frame -> True,
FrameTicks -> {Automatic, {Range[0, 100, 10], None}},
FrameLabel -> {"Mathematics Scores", "Frequency"},
FrameStyle -> Directive[Black, 16], ImageSize -> 500,
BaseStyle -> {FontFamily -> "Times"}, AspectRatio -> 1/3]}F) Saudis Participants
sa = Position[nationality, "Saudi"] // Flatten;
age20to29 = Position[age, n_ /; 20 <= n <= 29] // Flatten;
age30to39 = Position[age, n_ /; 30 <= n <= 39] // Flatten;
age40to50 = Position[age, n_ /; 40 <= n <= 50] // Flatten;
online = Position[examtype, "Online"] // Flatten;
inperson = Position[examtype, "In-Person"] // Flatten;
age20to29online = Intersection[age20to29, sa, online] // Length;
age20to29inperson = Intersection[age20to29, sa, inperson] // Length;
age30to39online = Intersection[age30to39, sa, online] // Length;
age30to39inperson = Intersection[age30to39, sa, inperson] // Length;
age40to50online = Intersection[age40to50, sa, online] // Length;
age40to50inperson = Intersection[age40to50, sa, inperson] // Length;
table = {{age20to29online, age30to39online,
age40to50online}, {age20to29inperson, age30to39inperson,
age40to50inperson}};
rowTotals = Total /@ table;
columnTotals = Total /@ Transpose[table];
totalAll = Total[Flatten[table]];
tabletotals = {{age20to29online, age30to39online, age40to50online,
rowTotals[[1]]}, {age20to29inperson, age30to39inperson,
age40to50inperson, rowTotals[[2]]}, {columnTotals[[1]],
columnTotals[[2]], columnTotals[[3]], totalAll}};
TableForm[tabletotals, TableHeadings -> {{"Online", "Inperson", "Total"}, {"20-29", "30-39", "40-50", "Total"}}]
super ace
Online gambling thrills, but smart betting is key. Games like Super Ace offer fun and potential wins, but always play within your means and stay in control.
super ace
Loving the blend of tradition and tech in modern creativity. Tools like Ghibli AI let fans bring Miyazaki magic to life-just don’t forget the soul in the details.
super ace jili
It’s fascinating how games like Super Ace mix luck and strategy. The free spins and wilds really keep players engaged, especially with that high winning potential.
MCP AI
MCP’s structured approach to AI integration is fascinating-tools like MCP Os Automation show real promise for streamlining workflows and enhancing model performance.
AI Image To Video
Great article! It’s fascinating how tech like the AI Old Photo to Video Generator can turn stills into motion – almost like magic for content creators on the go.
iamanus.com
The future of AI is autonomy, and tools like Manus AI are pushing the envelope. For those looking for a similar yet accessible option, check out DeerFlow AI. Exciting times ahead!
subway surfers
Endless runner fans will love the thrill of dodging trains in Subway Surfers Games. The mechanics are smooth, and the challenge keeps you coming back for more.
JiliOK
Understanding odds is key in gambling, and platforms like Jili77 offer tools to help players make smarter bets. Their AI-driven insights can be a game-changer for casual and seasoned players alike.
Jili7
Loved the breakdown of patterns-makes you think about how platforms like Jili777 ph use similar logic to boost user engagement and gameplay strategies. Insightful take!
Best Free AI Websites
I’ve been using Best Free AI Websites to explore free tools for my projects. It’s a great way to discover new AI solutions without breaking the bank. Highly recommend!
JLJLPH
Online gaming platforms like JLJL PH are reshaping how we engage with casino-style entertainment, offering a seamless mix of slots, live dealers, and immersive fishing games for players across Asia.
Top AI Tools
Great article! It’s amazing how AI powered tools can elevate strategic thinking in poker and beyond-definitely streamlining decision-making for players and pros alike.
JiliPH
Online gambling needs smart risk management-JiliPH users should prioritize responsible play. For a secure start, check out Jili No1.
JiliOK
Scratch games are fun, but JiliOK takes it up a notch with its AI-driven gameplay and top-tier slots. Check out their site at JiliOK-it’s a whole new level of entertainment!
SuperPH26
Balancing fun and responsibility in gaming is key. SuperPH26 shines by offering immersive slots and live games while promoting mindful play-a great model for the industry.
swerte77
Loving the in-depth analysis on e-sports betting! It’s refreshing to see real data-driven insights. For those looking to mix luck and strategy, check out Swerte99 for a top-tier gaming experience with some thrilling casino-style action.
KingPH
Great insights! For those looking to elevate their gaming journey, the kingph win platform offers a royal mix of slots, live dealers, and secure play – perfect for both new and seasoned players.
winph99
Just tried out some slots and the live games felt fresh and fun-great for a casual play session. The interface is smooth and easy to navigate. Check out winph for a relaxed yet exciting gaming vibe!
ph987login
I’ve tried PH987 jili, and the gameplay is smooth and exciting-perfect for both casual and serious players. Definitely worth checking out for a top-notch experience!
superph11
Love the breakdown-strategic insights always hit home. If you’re into gaming, checking out Super PH adds real value, especially with their live dealer variety and solid deposit options.
ph login
Solid article! Thinking about mobile optimization is key – even in poker. Seamless interfaces, like those at PH Login, can really boost engagement & playtime – crucial for tournament success! It’s all about that user experience.
jljl login
Roulette’s randomness is fascinating, but building a solid foundation of any game knowledge is key. Resources like jljl9 login emphasize that – understanding account security & funds is crucial before even spinning! Good article.
pinas77 login
It’s fascinating how much strategy goes into games – not just luck! Thinking about registration as a first decision-like with Pinas777 Slot Login-is a smart approach to building skills. Solid foundation is key!
Ghibli AI
Creating Ghibli-style art is easier than ever, thanks to tools like 지브리 AI. It’s a magical way to bring Miyazaki’s charm to your own photos without the need for advanced skills. The emotional depth they capture is truly special.
ph987.com login
Interesting take on bankroll management! Understanding game mechanics, like PH987 Login password highlights, is key. A solid platform & analytics can really boost strategy, don’t you think? 🤔
plus777 login
That’s a fascinating point about game mechanics driving strategy! Seeing platforms like Plus777 log in focus on analytical tools for players is a smart move – really elevates the experience beyond just luck. It’s cool to see innovation in that space!
super ace
Solid article! Thinking about card game strategy, even in slots like super ace deluxe demo, understanding symbol weight (like those Aces!) feels key. Bankroll management is always crucial, though! Good read.
jljlph login
It’s easy to get carried away with online games! Understanding the basics – like secure accounts & managing funds – is crucial. Resources like phlogin can really help build that foundational knowledge & responsible play. Good article!
phdream login
Interesting points! Analyzing betting patterns is key, but a smooth platform really elevates the experience. I’ve been impressed with the user focus at phdream – seamless access is crucial for consistent play. Great article!
ph789
Solid analysis! The focus on live dealer atmosphere is key – it’s about more than just the game. Seeing that social interaction really elevates the experience. Considering a dive into PH987 casino for a truly immersive feel – dealer professionalism matters!
jlboss
Smart bankroll management is key, especially with so many tempting options these days! Platforms like jiliboss offer a huge variety, but remember to play responsibly & set limits. Fun first, always! 😉
jl boss app
Basic strategy’s about minimizing losses, right? Seeing platforms like jlboss app offer diverse games does change the risk/reward calculation. Fun to explore options beyond the standard table! Good security is key too.
jl boss slot
Interesting take on slot strategies! Seeing sites like jboss pop up shows how much the virtual sports world is evolving. Quick access & secure info are key – sounds like they’ve nailed that! Definitely worth checking out for pro tips.
jl boss games
That’s a fascinating take on longshot strategies! Thinking about seamless integration, platforms like jl boss games really seem to be prioritizing user experience. Easy access is key, especially with options like the jlboss app! Good insights.
phlwin app
Interesting read! Thinking about the tech side of things, a smooth experience is key. I’ve heard phlwin app login is really streamlining things with AI & fast payments – sounds like a game changer for Filipino players! Definitely worth checking out.
philwin
It’s great seeing platforms like philwin ph really understand the local gaming culture! Responsible enjoyment is key, and easy access to local payment options (like GCash!) makes it even better. Let’s keep the fun going, safely! ✨
phlwin app
Dice games are surprisingly complex when you really break down the probabilities! Seeing tech like that phlwin slot platform uses-instant funding & AI discovery-makes enjoying them even easier. Smart registration sounds great too! 👍
jiliboss
Basic strategy really shifts your perspective – it’s not just luck! Seeing how small adjustments impact outcomes is fascinating. Thinking of leveling up my game like becoming a “boss” – maybe checking out jiliboss legit for some inspiration & faster play! Great article!
99wim
Interesting analysis! Seeing patterns in lottery numbers is fascinating, though luck still plays a big role. Heard 99wim slot download is popular in Vietnam – maybe a bit of digital luck there too? It’s all about finding your edge! 😉
12bet casino
Chơi 12bet casino mà app chạy mượt, không lag như mấy web khác 😌
jl boss
Interesting points about bankroll management! Seeing platforms like jl boss slot download prioritize secure account creation & verification is a good sign for responsible gaming, too. It’s all about smart play!
jljlboss
Solid analysis! Seeing more localized platforms like jljl boss games cater to Filipino players is great – especially with secure verification processes. Interesting how preferences are shifting in the region!
2jl
That’s a great point about balancing skill & luck in shooters! Thinking about accessible platforms like 2jl app casino, ease of use is key-similar to intuitive game design, right? Fun & fair play matter a lot!
jljl77
It’s smart to approach online gaming with intention, like jljl77 emphasizes – mindful engagement is key! Setting boundaries before you play is a great idea. Is jljl77 legit for responsible fun? Seems like they’re trying a different approach, which is refreshing to see!
21jllogin
Interesting read! Bankroll management is key, and seeing platforms like 21jl login offer easy deposit options (like GCash!) definitely helps players stay disciplined. Solid analysis here!
365 jili
Interesting analysis! Seeing platforms like 365 jili app prioritize easy registration & secure logins is key for building trust. Seamless deposits (GCash, PayMaya!) are a huge plus for PH players too. Good insights!
user-260452
awesome
winph99
Interesting read! The focus on data & transparency at platforms like winph99 club really changes the game. KYC processes are a pain, but essential for secure withdrawals, right? Solid analysis here!
SharNUT
[url=https://detikoptevo.ru/]Шары на день рождения[/url] — они наполняют пространство радостью и цветом. Вы можете купить как готовые композиции, так и отдельные шары для декора — быстро, удобно и по доступной цене.
Вы можете выбрать шары с надписями, цифрами, именами или просто любимыми цветами. Всё, что нужно — решить, каким будет ваш праздник, а мы доставим шары вовремя.
Шары помогают сделать праздник личным, атмосферным и по-настоящему запоминающимся.
Сделайте заказ прямо сейчас — и создайте настроение, которое останется в памяти.
https://detikoptevo.ru/
Stevennew
Продвинутые специалисты используют seo xrumer https://www.olx.ua/d/uk/obyavlenie/progon-hrumerom-dr-50-po-ahrefs-uvelichu-reyting-domena-IDXnHrG.html, чтобы добиться высокой эффективности.
betpk22
Smart bankroll management is key, even with data-driven platforms like betpk22 vip. Seeing that legit PAGCOR license & focus on stats is reassuring – minimizing risk is always a plus when exploring new online casinos & slots!
apaldo
Reading about game strategy really highlights how much mental fortitude is key. It’s interesting to see platforms like apaldo online casino cater to that, with secure logins & local payment options – a solid foundation for focused play!
sunwin.io
Sunwin.io giờ không biết còn hoạt động không nhỉ? Thấy nhiều phốt quá. Chắc chơi ở sunwin.io cho an toàn, dù sao cũng là Sunwin mà.
jljl2025
Solid analysis! It’s smart how platforms like jljl 2025 are focusing on responsible gaming & security – legit sites build trust. A mindful approach is key for enjoyable strategic leisure, don’t you think? 👍
365jili
That’s a fascinating point about game security – so often overlooked! Platforms like 365 jili login seem to prioritize player protection with robust KYC & SSL encryption, which is reassuring. Makes enjoying those slots a lot easier! 🤔
jljl9
Interesting read! Considering variance in roulette, a solid platform is key. I noticed jljl9 offers easy Philippines-focused deposits – convenient! Check out the jljl9 app download for a streamlined experience & explore their VIP perks. Good security is a must, too.
phspin
Interesting analysis! Seeing platforms like phspin prioritize security with KYC is smart – builds trust. RTP is key, and local payment options are a huge plus for Filipino players! 👍
jljl775
Platform choice is key, and fast transactions really matter. Seeing options like GCash & PayMaya with jljl775 is a smart move for Filipino players! Check out jljl775 vip – streamlined registration sounds promising for a quick start. Solid user experience is a must!
aajl
That’s a smart approach to competitive gaming – verifying accounts builds trust, and higher limits are a nice perk! Exploring platforms like aajl vip could be a good move for serious players wanting a secure, high-stakes environment. Definitely a focus on strategy there!
legendlink
Volatility is key when I pick slots – high variance can be thrilling (and sometimes painful!). Seen some interesting approaches with platforms like legend link, focusing on balanced games. Secure login & KYC are a must these days, too!
uujl
Solid article! Bankroll management is key, especially with so many tempting options now. Seeing platforms like uujl legit focus on secure verification is a great sign for PH players. Responsible gaming first, always! 👍
ph646
Smart bankroll management is key in any online casino! Seeing platforms like ph646 games offer quick deposits (GCash, PayMaya!) & KYC helps build trust & responsible play. It’s good to see security prioritized alongside entertainment!
ubet95
Lottery stats are fascinating – seeing patterns (or lack thereof!) is key. UBet95 offers a modern platform for exploring games & quick deposits, starting at just 100 PHP! Check if ubet95 legit is right for you – secure transactions are a must these days. Hoping for good luck to all players!
legend link
Solid article! Thinking about bankroll management & game selection is key for long-term success. Regulatory compliance, like at legend link casino, builds trust-important for any platform. Good read!
vvjl
Interesting read! Thinking about risk/reward in roulette really mirrors the strategic game selection mentioned at vvjl game. Quick registration & funding sound key to enjoying those slots & live casinos! It’s all about maximizing potential, isn’t it?
19slot
It’s fascinating how easily we fall into patterns when gaming – chasing losses is so common! Seeing platforms like 19slot slot download prioritize responsible gaming & community is a great sign. Plus, easy access via app download is key!
phpopular
Interesting analysis! Seeing patterns is key, and a bit of luck helps too. 😉 I’ve been checking out phpopular casino – quick sign-up & local payment options are a big plus for maximizing potential wins! Fun stuff.
987ph
It’s fascinating how gambling reflects cultural values – the Filipino concepts of ‘swerte’ & adventure really stand out! Exploring platforms like 987ph club shows how gaming evolves, offering modern takes on classic thrills. A neat blend of tradition & tech!
legendlink
Interesting points about responsible gaming frameworks! Platforms like legend link download are increasingly focused on KYC & secure transactions – vital for trust & player protection in the Philippines. Good to see innovation!
taya99
Baccarat strategy is fascinating – understanding patterns can help, but it’s never a guaranteed win! Seeing platforms like Taya99 prioritize community & easy access with a taya99 download is a smart move for Filipino players. Seamless registration is key!
legendlinkmaya
Interesting points about responsible gaming! It’s great to see platforms like legend link maya game prioritizing security & compliance, especially with KYC procedures. A smoother login process is always a plus too!
jlbossgames
It’s great seeing platforms prioritize user security – that KYC process at jl boss games legit sounds thorough! Remember to play responsibly & set limits. Enjoy the fun, but prioritize wellbeing always. 😊
pokebet88
I enjoyed reading this article. Thanks for sharing your insights.
arionplay
Interesting points about bankroll management! Seeing platforms like arionplay club prioritize quick, local deposits (GCash, PayMaya) is smart for the PH market – accessibility is key for consistent play. Good article!
arionplay
Blackjack strategy is so fascinating – understanding those probabilities really changes the game! Seeing platforms like arionplay com focus on secure accounts & easy deposits (like GCash!) makes getting started much smoother too. Definitely helps focus on the fun!
jlff
That article really hit on the importance of understanding the game – reminds me of the classic casino feel JLFF aims for. It’s about strategy, not just luck! Check out the jlff app for a taste of that golden age, especially if you’re in the Philippines – a solid platform to start with.
jlff
That “velvet ropes” feel at JLFF is spot on – a real nod to classic casinos! Observing the table first, as they suggest, is key. A solid strategy & managed bankroll are vital-check out the jlff login to get started & play smart!
phlboss
Really interesting read! The focus on tech enhancing the gaming experience is spot on. I especially like the idea of AI recommendations – sounds like phlboss casino is leading the way with that! Definitely a game-changer for Filipino players. 👍
phlboss
Roulette’s randomness is fascinating – the math behind it is truly elegant! Seeing platforms like phlboss leverage tech for fair gaming & fast transactions is a big step forward. AI recommendations sound cool too – less scrolling, more playing!
legendlink
Scratch cards always felt like a quick thrill, but online options are leveling up the fun! I checked out legend link online casino and their easy registration with GCash is a game-changer. Seems like a great way to chase those legendary wins! ✨
legendlink
Interesting read! Analyzing past performances is key, but finding a reliable platform matters too. Heard good things about the ease of use at legend link login – quick registration is a plus for getting in the action! Definitely worth checking out.
ph778
It’s fascinating how easily accessible gaming has become, especially in the Philippines. Platforms like ph778 club prioritize verification – a smart move for both security & responsible play. Understanding those initial steps is key for a good experience!
ph778
Baccarat strategy is fascinating – understanding patterns can help, but discipline is key! Seeing platforms like ph778 link prioritize secure, verified accounts is reassuring for serious players. Good user experience matters a lot, too!
jljlph
Understanding the psychology of gambling reveals how platforms like jljl craft immersive experiences, blending chance with strategy to keep players engaged.
jljlph
Trying out new games is always fun, and platforms like JLJLPH Login make it easy with their great selection of slots and live games. The seamless login and deposit process really enhance the overall experience.
77ph
It’s smart to be cautious with online platforms – security is key! Seeing sites like 77ph prioritize verification is a good sign. Explore responsibly & check out the 77ph app download if you’re curious about their games & community! Fun, but stay vigilant.
77ph
Understanding baccarat patterns is key, but remember responsible gaming! Platforms like 77ph link emphasize a fun, secure experience – crucial for any player. Exploring different games is a great strategy, too!
77ph
Understanding baccarat patterns is key, but remember responsible gaming! Platforms like 77ph link emphasize a fun, secure experience – crucial for any player. Exploring different games is a great strategy, too!
bigbunny
Interesting analysis! Seeing platforms like bigbunny apk prioritize provably fair gaming with blockchain tech is a smart move for building trust – especially with quick PHP settlements. Transparency is key!
bigbunny
Interesting read! Seeing platforms like BigBunny prioritize quick PHP settlements (GCash/PayMaya) is a huge plus for Filipino players. Considering a bigbunny slot download to check out their provably fair games – security is key these days! 👍
ph sky
Interesting analysis! Seeing platforms like ph sky casino prioritize responsible gaming & local payment options (GCash, PayMaya) is a huge step for Filipino players. Good stuff! 👍
ph sky
Interesting read! Balancing risk & reward is key, whether it’s in strategy or choosing a platform. I like that ph sky online casino focuses on responsible gaming & quick account setup – essential for a good experience.
pesowin
Interesting read! It’s smart to see platforms like pesowin vip focusing on player wellbeing alongside entertainment – crucial for responsible gaming. Understanding the psychology behind the games is a game-changer!
pesowin
Dice games are fascinating – the math behind them is surprisingly complex! It’s cool to see platforms like pesowin app casino emphasizing responsible gaming & wellbeing alongside the fun – a balanced approach is key, right? Definitely a plus!
747live
Smart bankroll management is crucial in tournaments, especially with varying stack sizes. Seeing platforms like 747live login offer easy deposit options (like GCash!) makes getting in the action smoother. Solid verification builds trust too – important for any legit site.
747live
Responsible gaming frameworks are crucial, especially with platforms like the 747live club emphasizing accessibility. Verification steps, as they detail, are a smart move for both players & operators – building trust is key! It’s good to see legit platforms prioritizing security alongside fun.
peryagame
Smart bankroll management is key, especially with so many options now! Seeing platforms like peryagame casino cater specifically to Filipino players with easy GCash deposits is a good sign. Remember, “Laro ng Puso” shouldn’t mean betting your heart and wallet! 😉
peryagame
Interesting read! Seeing platforms like Peryagame embrace local traditions and modern tech is smart. Quick registration & peso transactions are key for Filipino players! Check out peryagame download apk for a seamless experience. What games are you most excited to try?
jljl login
Solid article! Building a good foundation is key in any game, especially understanding account security. It’s great to see resources like jljl5 login emphasizing that – essential for newcomers & responsible gaming habits. 👍
jljl login
Scratch cards are such a fun little thrill! It’s cool to see platforms like jljl login focusing on how to approach online gaming responsibly – building that foundation is key, especially with finances! A smart approach to fun. ✨
2jl
Interesting read! Variance is a killer, but solid platforms like 2jl vip seem to prioritize a fair, RNG-driven experience. KYC is a pain, but essential for secure withdrawals, as they highlight. Good analysis!
2jl
That’s a solid point about team dynamics! Seeing platforms like 2jl legit focus on secure logins & verified accounts gives me confidence in fair play, which is huge for competitive betting. Good analysis!
TrevorNes
Когда нужно узнать что-то новое про авто, всегда читаю Автоновости. Информация достоверная и актуальная.